Radiation Impedances of Wire and Rod Antennas
Many readers of antenneX articles are in pursuit of the “holy grail” of electrically small, wideband, efficient antenna structures. This article attempts to explain the physical limits of electrically short wire and rod antennas, which necessarily have low radiation resistance into which it becomes increasingly more difficult to couple significant power as the length/wavelength ratio decreases. The article is also short, with links into wider reading.
“Short Defined”
An “electrically short” antenna has wires or rods which are short compared to a wavelength at the frequency of interest. Often, this means the individual rods are short compared to a quarter-wavelength. This does not mean that the structure itself is small; an antenna of rod length 100 metres would be “electrically short” for use at a frequency of 200 kHz. Neither does it mean that short antennas (physically) are necessarily “electrically short” if the frequency is high enough. A quarter wave monopole at a mobile phone frequency of 1.8GHz is only 4.2 cm long, or under two inches.
The mathematical expression Z = R + jX indicates that a circuit model may be made of a resistance R in series with a reactance X, with the same current flowing through each. The power delivered by a current of peak amplitude I and some phase angle to the impedance Z is, as remarked elsewhere, II*R/2, and does not depend on the reactance X which merely alters the terminal voltage V = ZI = (R+jX)I for a given supplied drive current I. On the other hand, there is a reactive power flow to and from the reactance X twice a cycle, and this reactive power flow is represented by II*X/2 .
The energy transferred to the antenna and its environs by the reactive power flow is stored mostly in the reactive near field. The energy transferred to the antenna by the resistive power flow either (A) heats up the antenna structure (or things in the near-field region of the antenna), or else (B) it is radiated, or (C) most usually, some of each. Thus we can break down the resistive part R of the driving point impedance into the sum of a loss resistance, Rloss, which gets hot, and a radiation resistance, Rrad. As the purpose of an antenna is to radiate energy, it is therefore the radiation resistance Rrad which is most interesting. Explicitly,
R = Rloss + Rrad
Calculating Resistance
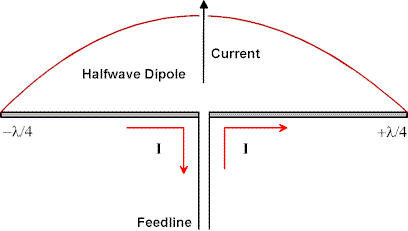
The classical way to calculate the radiation resistance is to surround the antenna with a hypothetical closed surface in the far field, calculate the values of electric field and Poynting vector on this surface in terms of the antenna terminal current I, integrate the power flow per unit area, represented by the Poynting vector, all over this surface, to determine the total outward travelling power in watts, and equate this power to the quantity II*Rrad/2 as discussed above.
If one does this one finds that the radiation resistance for a thin half wave dipole is about 73 ohms, with a reactive part that depends sensitively on the dipole rod diameter, of a few tens of ohms. If one takes a fat half wave dipole, the radiation resistance can fall below 60 ohms. Note that this radiation resistance is the same for all half-wave dipole antennas, whatever the value of wavelength. Unless you know what frequency the antenna is being used for, you have no way of knowing what the radiation resistance may be, just from knowing its physical size.
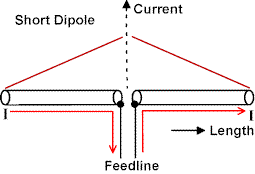
Now the contribution to the radiated electric field at a point in the far field region from a current I in a small physical length L of antenna wire is proportional to the time rate of change of IL and, at a given frequency, we can make this contribution larger in two ways; either increase I or increase L. Since free space is a linear medium, the principle of superpostion holds, and we find the total contribution to the radiated electric field strength by summing (or integrating) over all the little elemental contributions. It is accelerated charge which radiates, and the radiation contribution is proportional to the amount of charge times its acceleration. Dimensional analysis shows us that this is (Coulombs)(metres)(seconds^-2). We also see that the time rate of change of a current times an element of length is also (Coulombs/second)(metres)(seconds^-1) which is, when rearranged, just dimensionally equivalent to the accelerated charge.
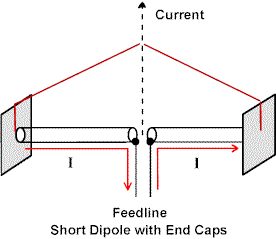
For a short thin wire or rod antenna, with L much less than a quarter wavelength, I falls away linearly or uniformly to zero at the end of the rod. If the rods have plates at the ends in the form of a capacitor, then the current I may not fall to zero, since it supplies the displacement current drawn from the plates.
In any event, the far field electric-field strength will then be proportional to the length of the rods, for a given terminal current, and if we square the electric field and integrate to get the power, it is clear that the radiated power must rise (for a given terminal current) as the square of the rod lengths. Thus the radiation resistance must be proportional to L^2, and indeed, looking in the standard textbooks we are presented with the formula that
R = 80*[(pi)^2]*[(L/lambda)^2]*(a factor depending on the form of the current distribution)
The factor depending on the current distribution turns out to be [(average current along the rod)/(feed current)]^2 for short rods, which is 1/4 for a linearly-tapered current distribution falling to zero at the ends. Even if the rods are capped with plates, this factor cannot be larger than 1.
Thus we can make a table for short dipole rod antennas. L is the total length of the antenna. (for monopoles above a perfectly conducting ground, the total length and the radiation resistance are both half of the values in this table)
| L/lambda | R (ohms) about |
|---|---|
| 1/5 | 8 |
| 1/10 | 2.0 |
| 1/20 | 0.5 |
| 1/50 | 0.08 |
| 1/100 | 0.02 |
Thus on 160 metres, if we erect a vertical monopole antenna which is 8 metres (26.7 feet) tall, the monopole length is 1/20th of a wavelength, and the radiation resistance will be half that for a 16 metre dipole (that is, L/lambda = 1/10). Our monopole has radiation resistance of 1 ohm. It also has a large negative reactance, depending on the rod diameter.
So, as the rod antenna is shortened, the size X of the (negative) reactance shoots up, as the antenna starts to look like a capacitor whose capacitance gets smaller as the size decreases, and so, for a given current, the terminal voltage rises sharply. It is for this reason that short antennas are very inefficient radiators; not only do they have low radiation resistance and require more current drive, but they present a serious mismatch to the resistive characteristic impedance of the feeder. Also, the higher currents required for a given radiated power dissipate more heat in the resistive loss in the skin-effect of the antenna structure, and so the efficiency drops. Even if the large capacitative reactance is tuned out successfully, the antenna then becomes inefficient, narrow-band, and prone to mistuning and mismatch problems by any alteration of the disposition of scattering objects in the near field.
Essential Dimensions
WHY does an antenna need to have dimensions comparable to a wavelength in order to radiate efficiently and with reasonable radiation resistance? It has all got to do with time delays and phase shifts across the structure. If we take a very small dipole structure; for example, consider the variable air-spaced tuning capacitor in many Ham transmitters, the distance from the connections, through the structure, to the furthest point on the plates, is very much less than a quarter wavelength. Thus, the voltage at the terminals is very nearly in phase-quadrature with the current drawn from them. This is as it should be for a capacitor. As we increase the frequency, there comes a point where this distance equals a quarter wavelength at the signal frequency. The capacitor then looks like a short circuit; it is self-resonant; the reactive part of its impedance falls to zero and it may be that it radiates rather well, with sizeable radiation resistance. Travelling waves have been set up on the capacitor; the reflected wave has travelled twice lambda/4, that is an exact half wavelength, so its phase is reversed and the reflected voltage added to the incident voltage gives zero – a short circuit. Whatever the current supplied by the feeder, the capacitor (if it doesn’t radiate any power) looks like a resonant series combination of a C and an L. The negative reactance of the C just cancels the positive reactance of the L, and the combination (at that particular frequency) is a short circuit. The current flowing into and on the capacitor structure generates a magnetic field which stores energy in the L reactance.
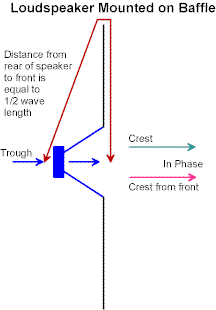
IN an antenna we put phase-delay to good use, to bring the terminal voltage more in phase with the terminal current. Now we can see why there is this “magical” figure of a quarter-wavelength; for the reflected wave has to be altered in phase significantly with respect to the outward wave.
IF you still have difficulty with the concept of “antenna structures providing phase delay”, consider the performance of a 1950s hi-fi loudspeaker on a baffle. A baffle used to be a sheet of wood, with a hole cut in the centre for the loudspeaker, and several feet across from the loudspeaker axis to the edge of the wood. The objective of this arrangement is exactly the same as the objective of making an antenna larger…..to increase the time delay that it takes for the reduced pressure at the back of the speaker to arrive at the increased pressure at the front (when the cone moves forwards).
Ideally one would like this transit time to be half-a-cycle, so that the contributions add at the front. Thus, putting in the numbers, a 2 metre square baffle would have a transit time of 6.6/1100 seconds = 6 milliseconds from back to front (the speed of sound in air is about 1100 feet per second) and that provides half a cycle at a frequency of 1000/12 Hz = 83.3 Hz, enhancing the bass output considerably. Without the baffle, if the speaker diameter was 8 inches, the transit time would be at most 0.66/1100 seconds or 0.6 milliseconds and the frequency response would fall off rapidly below 833 Hz. Try it and see.
YOU can also (being keen electronics measurement people) drive such an arrangement at say 500 Hz, and measure the voice coil impedance with and without the baffle. You will find that the resistive part of the impedance rises appreciably when the baffle is added to the loudspeaker configuration.
IN FACT, we are very fortunate in the real world that electrically small structures cannot be made to radiate well, as it is far more commonly the case that we want to prevent our apparatus from radiating in a promiscuous manner, and this is easily arranged by keeping the apparatus sufficiently small.
Originally posted on the AntennaX Online Magazine by Dr. David J. Jefferies
Last Updated : 27th May 2024
