3 Wires WorldWide! Without a Rotator
Many folks are fond of vertical antennas, especially below 14 MHz. These antennas take up little horizontal real estate. With a little ingenuity, we can make them from wire. By using vertical dipoles, we can save the pain of laying a ground plane. And we can work the world without a rotator! The low elevation angle of maximum radiation is not only good for DX, it is also a natural filter from QRM and QRN originating closer in.
If there are problems, they number two: 1. The antennas have low gain, and 2. We need either a braced vertical or something high from which to hang the long wires. I can help a bit with the first problem, but the second is yours. If you have some tall trees, you might consider hanging support ropes as high as you can go and suspending your vertical dipoles from them. Tall towers for upper HF beams can also serve as anchors for a vertical array.
However, let’s keep the gain requirements modest—say about 3 dB more gain than from a single vertical dipole. But let’s also keep active our aim of working the world. Assuming that we can hang 3 wires, we can make a nice little triangular parasitic array that will do just the job we need.
The Basic Layout
For 40 and 30 meters, wire vertical dipoles become quite practical. At about 10′ off the ground, they show a take-off angle of about 16 degrees, and have something over 1 dBi gain. But they are tall, with a 40-meter vertical reaching almost 80 feet and a 30-meter vertical stretching above 55′ up.
If we can manage the height, we can build a switchable directive parasitical array from 3 wires. Figure 1 shows the general layout. Essentially, the system consists of three verticals laid out so that two form parasitical reflectors for the third, which is a driven element. The parasitical arrangement is capable of about 3 dB gain over a single vertical and yields between 15 and 16 dB front-to-back ratio without any effort expended on calculating and pruning a phasing system. If these benefits are sufficient, then we can proceed.
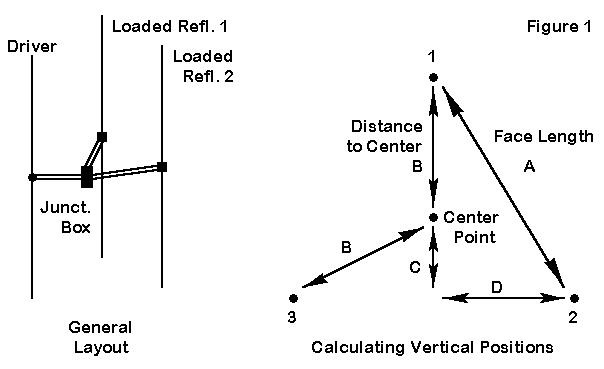
The right side of Figure 1 shows the way to calculate the positions of the three elements in an equilateral triangle. If we know the face length, A, then the others will fall in place this way:
B = .577 A
C = .289 A
D = .5 A
How large shall we make A? Actually, the length of A depends on two factors, neither of which is some special fraction of a wavelength taken from theory. Letting the distances between verticals run from 0.12 wl to about 0.25 wl yields nearly the same gain with about the same front-to-back capability (using parasitical arrangements). So what might set our distance?
First, the driven element will have to be shortened from its natural resonant length when isolated as a dipole. We shall shorten all three legs accordingly, since each will serve in its turn as the driven element. However, reducing the length of all the wires will require us to load the two legs to make them act as reflectors. We can do this the hard way with loading coils, or we can do it the easy way with shorted coax stubs. We shall bring the stubs to a central junction box, where the reflector stubs will be shorted and the driver stub becomes just another short length of the feed system. In this way, we can use a remote switch and some relays to change the direction of the array. So, the length of the feedline used as a shorting stub helps to determine the length B, since we may wish to bring the line directly to an elevated box centered among the 3 wires.
Second, the face length A determines the feedpoint impedance of the driven element. When the face length A is about 0.16 wl, the source impedance of the driver approaches 50 Ohms, a very handy value indeed. At 7.1 MHz, this distance is about 22 feet. With this face length, the distance B becomes about 12.7 feet. Will the loading stubs be at least this length for the assembly? Actually, we get a little length to spare. The required stub for 50-Ohm, 0.66 velocity factor line will be 16.4′ long, enough to allow some play in the line for a direct connection.
For those unfamiliar with calculating the length of shorted stubs, the basic equation for determining the inductive reactance from the length of transmission line is
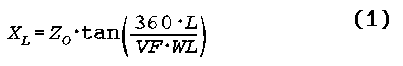
where L is the line length and WL is a wavelength, both in the same units, VF is the velocity factor of the line, ZO is the line’s characteristic impedance, and XL is the inductive reactance. Solving for L, the line length, we get
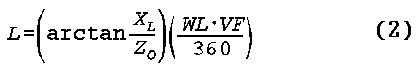
where the terms have the same meaning as in equation 1. If we want to place the junction box on the ground, we can add a half wavelength of line (taking the velocity factor into account) and achieve the same reflector loading goal.
Some Dimensions
Here are some starter dimensions for both 40 and 30 meters, assuming that each antenna starts 10′ off the ground.
Triange factors (measured in feet)
| Frequency (MHz) | A | B | C | D |
|---|---|---|---|---|
| 7.1 | 22′ | 12.7′ | 6.35′ | 11′ |
| 10.1 | 15.5′ | 8.95′ | 4.47′ | 7.75′ |
Antenna Wire (#12) and cable factors (measured in feet)
| Frequency (MHz) | Vertical Length | Top Height | Stub Length (RG-213) |
|---|---|---|---|
| 7.1 | 65.9′ | 75.9′ | 16.4′ |
| 10.1 | 46.325′ | 56.325′ | 11.7′ |
If you move up or down from the given vertical positioning, expect some small changes in the required dimensions, but none so great that you cannot make the system work.
The Switching System
The beamwidth of the triangle array is between 128 and 130 degrees wide between -3 dB power points. Since 120 degrees is one third of the horizon, switching the elements around between driver and reflector functions will cover the horizon in three switch positions.
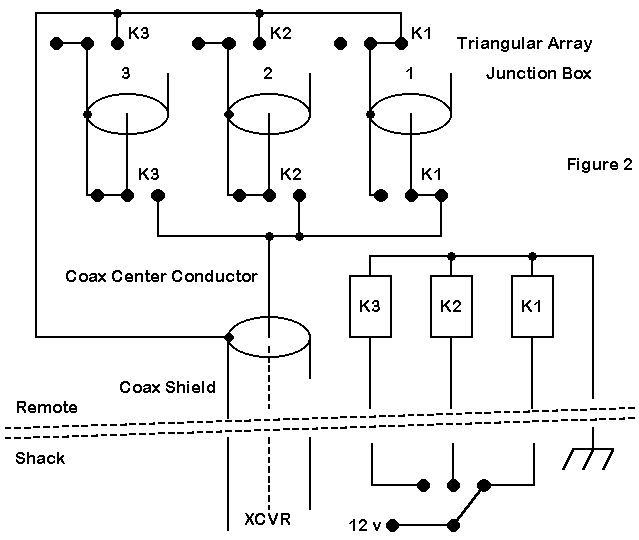
Figure 2 shows a simple switching system for the array involving three DPDT relays. The schematic shows antenna 1 as the driver, with verticals 2 and 3 having shorted stubs. Note that the stub shields or braids are isolated from the main feedline braid when the stubs is shorted. When a stub becomes an extension of the feedline, its braid is connected to the feedline.
The relays can be anything from small items purchased locally for low power use to beefy units for high power operation. The components require a waterproof box, but the coax connectors should not be directly grounded to the case, since that would defeat braid isolation. In addition to the usual coax feeder to the shack, a 4-wire rotator cable (or a similar cable suitable for outdoor use) carries power to energize the relays, according to the switch position in the shack. Of course, at the shack end of the line, you can make up any desired indicator system, from a simple row of LEDs to a small map with the lamps showing the part of the world at which the array is aimed.
In the schematic, when no power is applied (that is, when the station is idle), all relays revert to the shorted stub mode, and the feedline is disconnected from the three vertical wire dipoles. You may add whatever other safety features you deem appropriate to the junction box system.
Performance
How well can we expect this very simple array to perform? The answer lies in some properly interpreted far field plots.
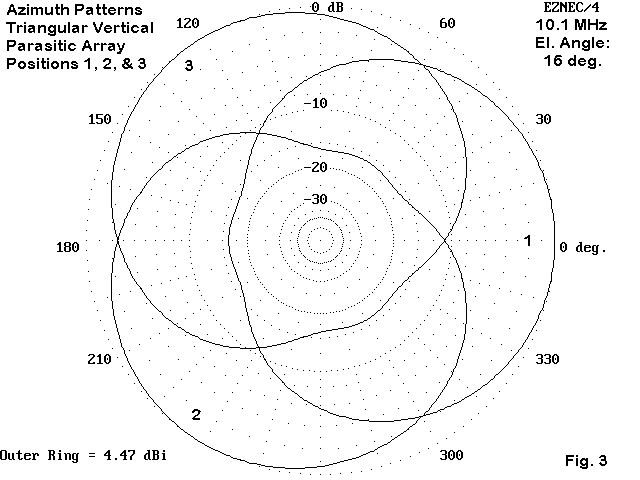
Figure 3 shows an overlay of the three possible azimuth plots, one for each switch position. However, do not take these plots completely at face value.
First, note that there are slight nulls in the coverage. Although they are shallow, you may wish to orient the array so that the nulls point at places where no ham lives.
Second, the gain figure holds only for placement of the antenna over average ground. As the soil gets either better or worse in the general category scheme, the gain will rise. (The actual pattern of gain vs. height above various soils grows more complex as we take into account more varieties of coil conditions.) However, the improvement over a single vertical wire will remain about constant. Although “average soil” yields nearly the lowest gain figures of any soil (depending upon the exact vertical height over it), the take-off angle will decrease as the soil improves and will rise as the soil condition grows worse, almost wholly independent of the gain.
Third, the figures show the slightly higher gain figures yielded by the 30- meter version of the array. 40-meter gain figures are about 0.15 dB lower due to the lower effective height of the antenna, since we placed each at a minimum height of 10 feet.
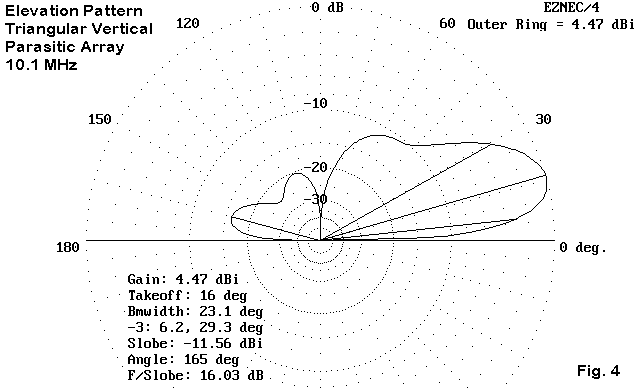
The elevation plot shown in Figure 4 shows the vertical array benefits to their best advantage. The low take-off angle favors DX skip angles, while the front-to-back ratio is very useful, if somewhat short of astounding.
The absence of significant high angle lobes, including the total absence of one directly overhead, is also beneficial for communications, since QRM and QRN originating at short skip distances are naturally attenuated, relative to a horizontal dipole or similar antenna. (However, this feature does not affect local area noises, many of which are vertically polarized.)
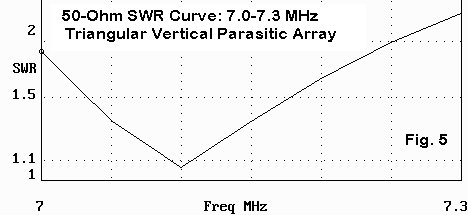
The SWR curves for the arrays are good (but not perfect) for 40. Sliding the design center frequency a bit higher or lower than 7.1 MHz will allow coverage of a desired band edge. As you move lower than the design center frequency, the pattern loses some front-to-back ratio, but adds a bit of gain. Higher up, the gain drops, but the front-to-back ratio is sustained.
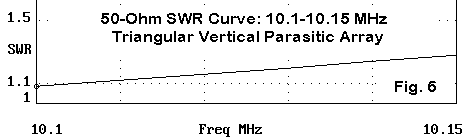
Within the narrow confines of 30 meters, SWR is no problem at all. The band is not wide enough for the pattern to change significantly.
Conclusion
The triangular array can be scaled and adjusted for many bands. For example, a 10-meter version might be mounted on a single mast with three 5′ PVC arms supporting the 3 vertical dipoles. In this case, the dipoles might use some combination of 3/4″ through 1″ hardware-store aluminum tubing. VHF versions can be even more compact. When the antenna is several wavelengths above ground, the low-angle gain increases considerably while retaining the wide beamwidth that offers full-horizon coverage in 3 switch positions.
ON4UN, in his justly famous Antennas and Techniques for Low Band DXing, devotes an entire chapter (11) to phase-fed vertical arrays. However, vertical Yagis, that is, parasitical arrays, receive scarcely 1 column of attention (in Chapter 13). Granted, a correctly phase-fed vertical array is capable of a very deep 180-degree null. However, the overall front-to-rear ratio may not for many operators be sufficiently superior to that of a parasitical array to justify the effort of perfect phasing. In addition, the perfect null does not occur at the same phasing among elements as maximum gain, and the gain difference may approach a full dB.
Those who prize the silent rear will continue to phase-feed their systems carefully. However, those who prefer simplicity in their installations may wish to explore parasitic techniques to achieve a compromise between gain and front-to-back ratio. Ted Hart, W5QJR, showed a 5-wire design a few months back in these pages. You might consider this 3-wire array the little brother of his system, since it is essentially a 2-element vertical Yagi with a double reflector. Like the bigger system, with proper switching, it will cover the entire horizon with a bit of gain and some useful front-to-back ratio.
Of course, for many, the required height to implement this system may be out of reach. Many of us use verticals that are considerably shorter than a full 1/2 wl long. As I shall try to show in a later item, all is not lost: there are triangular possibilities for the short vertical operator.
Update - One Month Later
A Triangle for the Short Vertical Operator
Last month, I described a triangle array of three full-size vertical dipoles for 40 meters (with 30 meters as a bonus). Since these wires require that we have access to supports around 80′ up, I promised a triangular array composed of short vertical elements. Time to keep my promise. We shall design a 40-meter triangular array of three hatted dipoles having a total height of 22′ above ground, with the bases 4.5′ off the ground. Even if you do not need such an array, the techniques involved may be useful to you somewhere else down the road. For some of the background material, I shall rely on last month’s item. We need the space this month for current detail. So I hope you saved a copy of the tall triangle.
Hatted Dipoles
When a dipole is shortened, it maintains far more of its gain potential than most folks realize. Of course, in its shortened condition, it is no longer at or near resonance. Hence, we load it. Inductive loading of a dipole, whether placed at the feedpoint or moved to a mid-element position, creates the greatest loss, since either method converts high current areas of the linear element into tightly confined inductive fields, leaving lower current on the linear element beyond. Even with no resistive coil losses, the gain drops well below that of a “hatted” dipole.
Figure 1 shows a very short hatted vertical dipole next to its full-size counterpart. In free space, the hatted dipole has a gain of only 0.35 dB less than the full size dipole. Since the radiation pattern strength is a function of the current on the antenna, and since the hatted dipole preserves undisturbed the high current portion of the dipole element, it also preserves most of the dipole’s far field pattern strength.
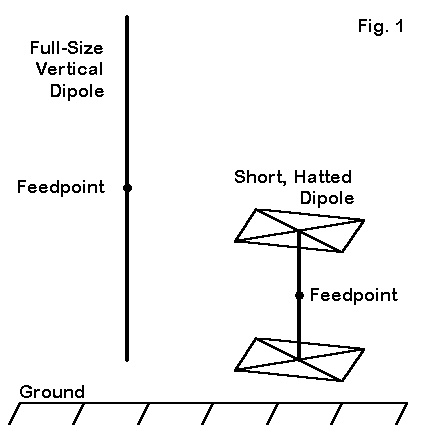
Brought near the ground, as we propose to do in this exercise, the hatted dipole shows some further far field weakening compared to the full size dipole. With a base of 10′ from the ground and a feed point about 32-35′ above that point, the full size dipole has a 1.3 dB gain over the hatted dipole set only 4.5′ above ground with its feedpoint less than 9′ above that point. The difference also shows up in the elevation angle of maximum radiation: 16 degrees for the full-size dipole vs. 26 degrees for the hatted dipole.
A triangular array of hatted vertical dipoles is capable of a forward gain of about 2.5 dBi, about 2 dB less than a similar array of full-size dipoles. Most of the gain decrease comes from the lowered height of the feedpoint and the element region immediately surrounding it. But remember that the entire hatted dipole array vertically does not even reach the feedpoint of the full size dipole array. Moreover, the array shows a gain of abut 3.6 dB over a single hatted dipole. If we can only manage short verticals, then the triangle offers significant gain and directionality over the single short vertical.
A triangular array of dipoles only 17.5′ long, with bases about 4.5′ off the ground, gives us something we might control mechanically without upper support requirements. We might construct the elements from 1.25″ aluminum or similar material. Of course, we shall need to consider the hats for both the top and bottom ends before we are done.
For the present design, I enlarged the triangle face to about 35′ for element spacing that is closer to 1/4 wavelength. The center point amid the elements is 20.25′ from each element. (See last month’s “3-Wire” item for details of figuring an equilateral triangle.) The reason for increasing the spacing is to broaden the operating bandwidth of the array, since shortened elements tend to decrease operating bandwidth, even with symmetrical hats which preserve operating bandwidth better than any other short element loading form.
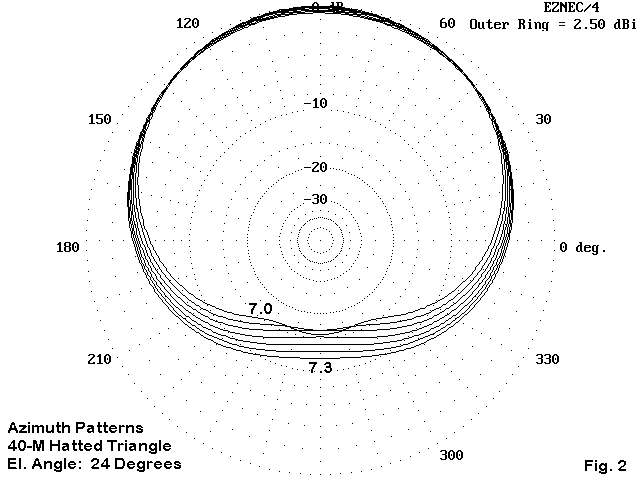
The pattern characteristics of the triangular array remain quite good across 40 meters, as illustrated in Figure 2. The anticipated front-to-back ratio varies between 11 and 16 dB across the band, while the gain varies by less than 1/2 dB. Therefore, if the lower gain and somewhat higher elevation angle of maximum radiation are acceptable, then this array is worth further consideration.
Each element will consist of a 17.5′ conductor of moderate diameter. 1.25″ is a good design start, although you will use what is most conveniently obtained. You will also need insulated pipe or tubing for the center or feedpoint separator and for the base mounting support.
Figure 3 provides some of the rough details for a hatted vertical dipole. Each dipole will have a loading/beta inductor at its center. When the element functions as a reflector, the inductance loads the element to the correct electrical length for nearly optimal reflector functioning. When the element operates as a driven element, the same inductor functions as a beta match reactance. The elements are cut specifically to a length that, when set in a triangle of the size prescribed, shows a feedpoint impedance of 30-35 Ohms resistance and about 20 Ohms capacitive reactance at the center of 40 meters. The reactance at the center of each element is about 60 Ohms.
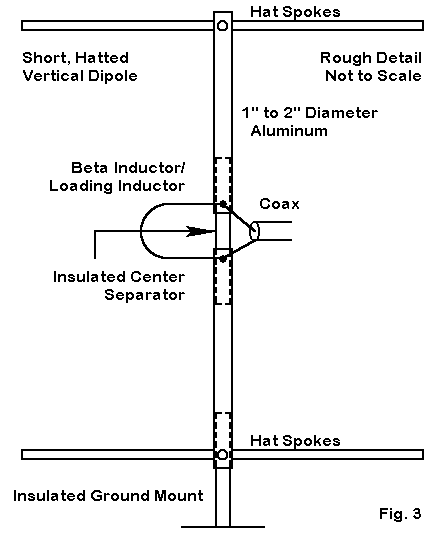
The original design used 1/8″ rods for the capacity hats, with similar material used as a perimeter wire. The hat structures use an 8.4′ spoke length. The large 4-spoke hats are only one possible hat design. There are numerous ways to fasten rods to the main mast. You can drill through the main element. Alternatively, you can create a bracket to both support the rods and fit over the main element. Construction details are largely a matter of locally available materials and builder comfort in using them.
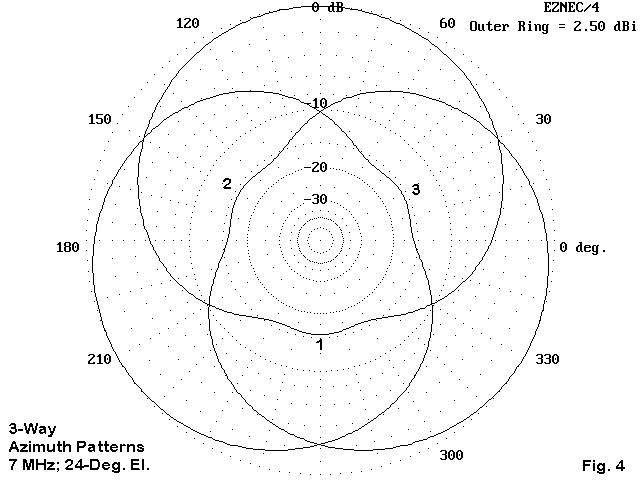
The array provides three-way coverage that is essentially the same as the full size-array, as shown in Figure 4. Half-power points are separated by about 130 degrees so that little is lost to the nulls between peaks. Although the take-off angle is somewhat higher than with a full size dipole, there is considerable gain at lower angles for solid DX skip angle coverage on 40 meters. The antenna system provides full horizon coverage at a gain level similar to the fixed bi-directional gain of an optimized delta SCV.
Feeding the Short Triangle
Let’s spend a little time looking more closely at the load and feed system of the shortened elements. As noted, each element has a permanent 60-Ohm loading inductive reactance permanently attached across the insulated center of the element. The reactances are loads only when the element functions as a reflector, which occasions less loss than when a driven element is inductively loaded at its center. When the reactance is across the driven element, it is part of a beta matching system. Figure 5 shows the two styles of loading reactance that we can use.
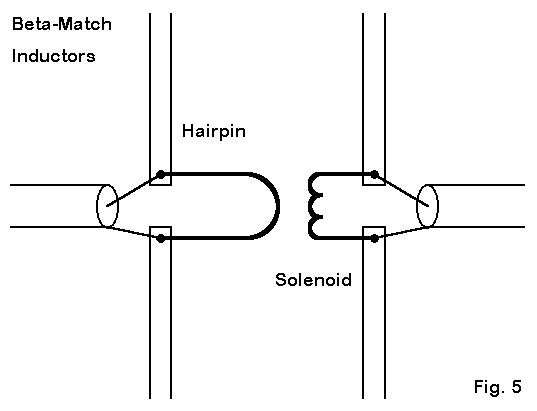
The hairpin is nothing more or less than a shorted section of parallel transmission line. You can fabricate your own, perhaps of #10 aluminum wire (to avoid bi-metallic effects at the junction). With a 2″ spacing, the hairpin will need to be a little over 2.9′ long. A 4″ spacing between wires shortens the length to about 2.5′ on the assumption of a velocity factor of 1.0 for these self-supporting lines. You may also use 450-Ohm parallel line, which would require nearly 2.8′ if the velocity factor is 0.95. 300-Ohm TV ribbon with a velocity factor of 0.8 calls for nearly 3.5′ of line.
For this application, a solenoid coil may be the most compact solution. There is insignificant loss if the Q is over 200, which is easily obtained from a coil that has well spaced turns and a diameter that is nearly equal to the coil length. 7 turns of #10 wire spread to a length of about 1.6″ will provide adequate “squeeze and spread” adjustment range for tuning up the system.
The next step is to control the elements so that each knows when it is a reflector and when it is a driven element. For this purpose, we can use 1/4 wl sections of 50-Ohm feedline. A 1/4 wl section of RG-213, and similar lines with a 0.66 velocity factor, figures to be about 22.6′ long when cut for the center of 40 meters. Since the distance from the element to the center of the triangle is 20.25′, these lines leave no room for flex and might require a central control box to be mounted at the 13.25′ feedpoint height–which is bound to be inconvenient. Foam lines, like RG- 8X, have a velocity factor of about 0.79, resulting in a 1/4 wl section that is about 27.2′ long. This length permits a nice slope to a few feet off the ground, with a bit of flex to spare. However, I have found foam lines to vary considerably is actual velocity factor, with one batch measuring at just over 0.73. Hence, test the 1/4 wl lines you cut before using them.
We shall press into service the very same control box we used for the full size array described last month and shown in Figure 6. The remotely switched relays connect the coax from the shack to one of the three 1/4 wl lines. Since, this makes the element a driver, the section from the box to the element is just another part of the feedline, and the reactance across the element feedpoint is a beta matching coil.
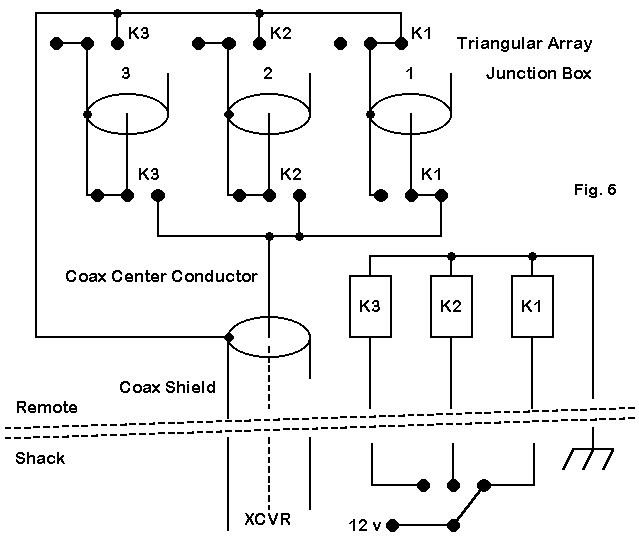
The other two 1/4 wl lines are shorted at the control box and not connected to either the center conductor or the braid of the shack feedline. When shorted at the control box, a quarter wavelength line section show a very high impedance–essentially an open circuit–at the element end. Now the coils at the center of each element provide continuity for the element and load it to the correct electrical length for use as a reflector.
Switching directions is as easy as with the full-size array. However, be sure to note the different electrical principles involved for the full and short arrays. All switches look alike, but what they switch may be very different things.
Hatting the Dipoles
The short dipole array is designed to set each element 4.5′ off the ground, for a maximum element height of 22′. Hence, each 17.5′ dipole is just about one-fourth of full dipole length. Hat structures may require as much horizontal room as the dipole takes up vertically. The original design used 4 spokes and a perimeter wire to connect the tips of the spokes.
However, hats come in many variations, from as few as 2 spokes set precisely in opposite directions to 60 or more symmetrically spaced spokes. As Figure 7 shows, the design may use spokes only or use a connecting wire from tip-to-tip. Each of these hats is symmetrical so that the radiation from one part is canceled by radiation from elsewhere in the hat.
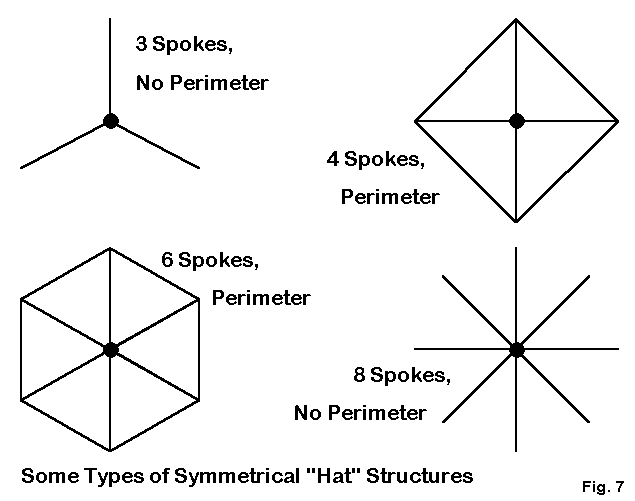
The relationship of the spoke length (which establishes a virtual hat “radius”) and the number of spokes is quite regular, although not simple. First, spokes are shorter, for any set number of them, if a perimeter wire is employed. The true element end is not at the tip of the spoke, but half way between spokes on the perimeter wire. Very roughly, the effective spoke length is the sum of the spoke and the half-length of perimeter wire.
Figure 8 shows a graph of what happens to the required spoke length as the number of spokes is increased–for both the spoke-only design and for the spoke-plus-perimeter-wire design. Although this study was done at 3 MHz, the trends are perfectly applicable at any HF frequency. For small numbers of spokes, the perimeter wire shortens the hat radius fully by half. However, as the number of spokes increases, the shrinkage benefit of the perimeter wire is reduced, since the length between tips is much shorter.
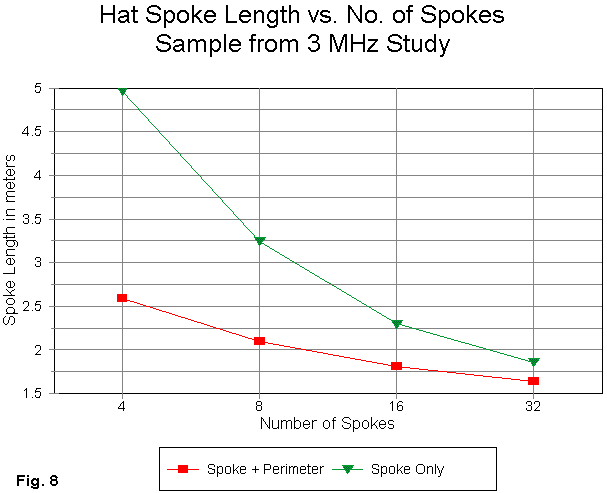
At the same time, more spokes means shorter spokes, but probably not beyond a limit of about 60 spokes, when the system begins to simulate a solid disc. You can draw out both curves on the graph until they intersect and level well beyond the right edge of the graph. Notice also that there is a minimum spoke length limit. This limit is about 70% of the spoke length of the 4-spoke-plus-perimeter design. Hence, for the triangular do not expect spokes much less than about 5.5′ long, no matter how many you add.
Actual spoke system construction once more is a local effort and depends on available materials and construction techniques you have mastered. You can, of course, use an insulated extension for the element to provide truss support for the upper spokes, and replicate something similar for the lower hat.
Alternative Hat Systems
If full 40 meter coverage is not required and slightly less gain is acceptable, you may construct more compact non-symmetrical hats to replace the symmetrical ones used in the original design. A non-symmetrical hat does not provide complete field cancellation from the hat structure, although tight coupling can reduce horizontally polarized radiation to levels 25 dB or more below the overall field strength.
Figure 9 shows some, but by no means all, options available for non-symmetrical hat design. The spiral, if very carefully constructed, can become a nearly symmetrical hat, although coupling between different points along the same wire prevents true symmetrical hat performance.
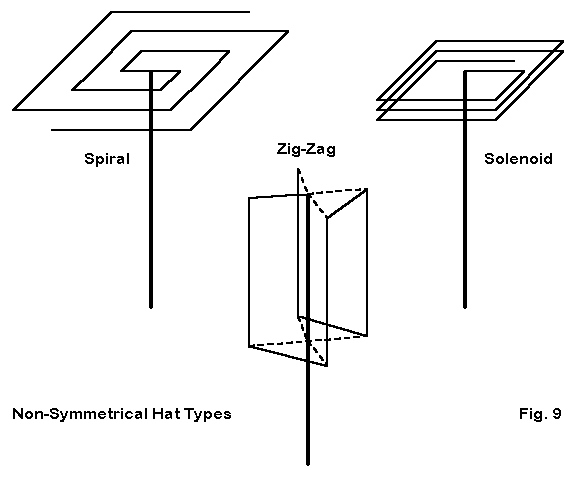
The solenoid, shown as a large spread coil, can also be compacted into a length of wire resembling a normal inductor. However, at the high-voltage, low-current end of the element, there are radically unequal currents at the coil ends, defeating the conditions required for an inductance of appreciable magnitude. Instead, the solenoid functions as simply a length of wire so configured as to minimize its physical size and to allow the element to reach resonance. (A measure of how little the end-loading solenoid acts as an inductor can be seen by comparing the actual coil of wire required to produce resonance with an inductor that might be used as a source of inductive reactance. Inductive reactance values in the 10s of thousands of Ohms are needed near antenna element ends to effect reactive loading, while the wire coil achieves resonance with only a small fraction of the wire length needed to make a coil with the high reactance. In antennas, not everything that looks like an inductor functions as an inductor. Similar things can be said of apparent capacitors.)
The zig-zag hat is simply a variant of extending the wire outward, but bringing it inward and then back and forth (up and down for a vertical element) until resonance is achieved. (The dotted lines in the sketch represent insulated supports.) The close coupling extends the total length of wire required to make this type of hat, but the wire can be light and held within about 2′ of the main element for fairly good efficiency.
Every form of non-symmetrical end loading offers both advantages and disadvantages. On the plus side is the fact that non-symmetrical end loading can result in quite compact antenna structures that are mechanically easier to fabricate and maintain. However, all such structures result in less gain, lower feedpoint impedances, and a narrower operating bandwidth for both the antenna characteristics and the feedpoint impedance. Wherever physically feasible, symmetrical hats are superior.
Conclusion
The array lends itself to considerable experimentation. One direction might be to off-center feed the dipole at the junction with the lower hat. Little change to the feedpoint impedance occurs in the few feet from center, and the reflector loading reactances and beta inductor will be about the same. However, there is a price to pay for the convenience of having the feedpoint and 1/4 wl lines so close to earth. There may be considerable current on the outside of the coax lines. Therefore, W2DU chokes may be needed, and the length of each one will be part of the 1/4 wl lines.
The short, hatted three-dipole array is certainly not for everyone with the backyard space for it. The array presents some construction challenges that may be beyond what a given situation permits. However, it does offer a number of design ideas that are worth stowing in the notebook for future reference. Hatted dipoles (and monopoles) offer superior performance to elements of equal length using other forms of loading. Elements, even with loads at their centers, can be made to perform different functions in a given array depending upon their connection–and that may be remotely controlled by fairly simple means. Triangles offer one of the least expensive steerable arrays for the lower bands.
While you may not build this array, I’ll bet at least one of these ideas works its way into your future antenna construction projects.
Originally posted on the AntennaX Online Magazine by L.B. Cebik, W4RNL
Last Updated : 16th March 2024
