Antenna Impedance Determination And Matching

Antenna Impedance Determination and Matching

Most amateurs understand the concept of matching impedances to maximize power transfer. It is straightforward when dealing with purely resistive loads which can easily be measured. Unfortunately, most amateur antennas do not fall into this category. It is usually difficult to build (and then install) an antenna system which does not exhibit reactance and is often very difficult to measure the antenna’s final impedance after installation (ground-mounted verticals are usually an exception).

Generally, if the impedance at the feed point of an installed antenna is known a network can be designed to correct any mismatch that may exist. Numerous matching networks and schemes such as the “series-section” have been described in various amateur publications’ over the years.

Impedance Determination

A method to ‘remotely’ determine the feed point impedance of an antenna has been previously described by William Vissers, K4KI (Sorry but the Callsign was not too intelligible on the original documentation). Mr Visser’s procedure is simple in that it uses only the impedance measured at the transmitter end of the coax (such as that obtained with a noise bridge) and the electrical length of coax. These values yield the antenna feed point impedance, via the following expression:

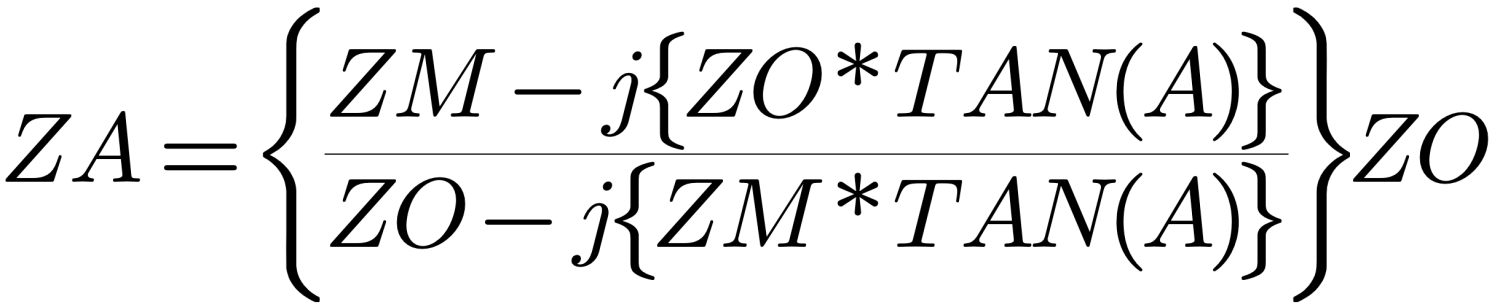
where

ZA = antenna feed point impedance
ZM = measured impedance at transmitter end of the coax
ZO = impedance of feed line
A = feed line electrical length in degrees (frequency dependant)
and j = the complex operator (i.e., square root of -1)

The difficulty with using this expression is that the impedance measured at the transmitter end of the coax (ZM) will almost always be complex, i.e., it will have reactive component as well as its normal resistive component. This complicates the math in the equation above somewhat, because ZM is now:

where

ZMr = the resistive, or real component
ZMi = the reactive, or imaginary component
and j = complex operator (as in the first Equation shown as Figure 1)

With a complex ZM, Equation 1 becomes:

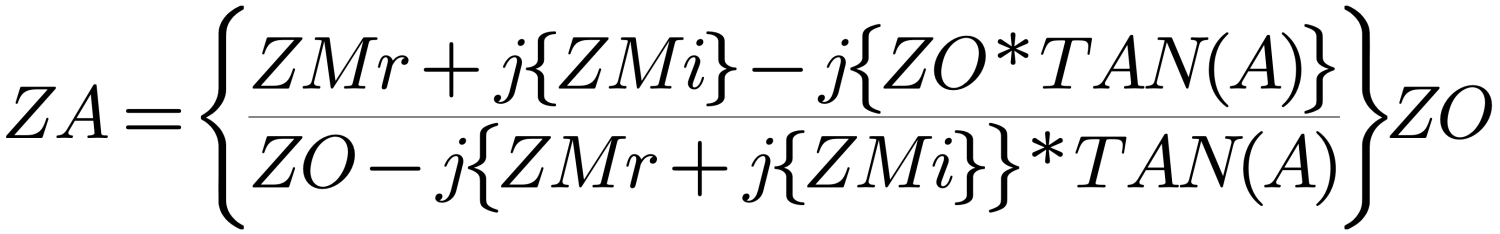
With a reasonable amount of care and a good hand calculator, Equation above (Figure 3) can be coaxed to yield a feed point impedance. This ‘manual calculation’, however, is tedious for repetitive calculations, so a means was sought to use a home computer for the calculations.

The first problem was how to deal with complex numbers on a home computer since suitable and inexpensive software to manipulate numbers isn’t readily available. The solution is to take the complex moth out of the problem.

Equation 3 (Figure 3) is broken into real and imaginary parts by removing the imaginary term from the denominator through the use of a math operation called ‘using the Complex Conjugate’. To illustrate this, the Complex Conjugate of A+j{B} is simply A-j{B}. Multiplying them together results in A²+B². There is no longer an imaginary term to tangle with. In addition, multiplying both the numerator and denominator of a fraction by the Complex Conjugate of the denominator is the same as multiplying the entire fraction by 1. It doesn’t change the value of the expression, but it does allow the removal of the imaginary term from the denominator.

The terms in Equation 3 (Figure 3) are first rearranged to separate the real and imaginary parts of the numerator and denominator:

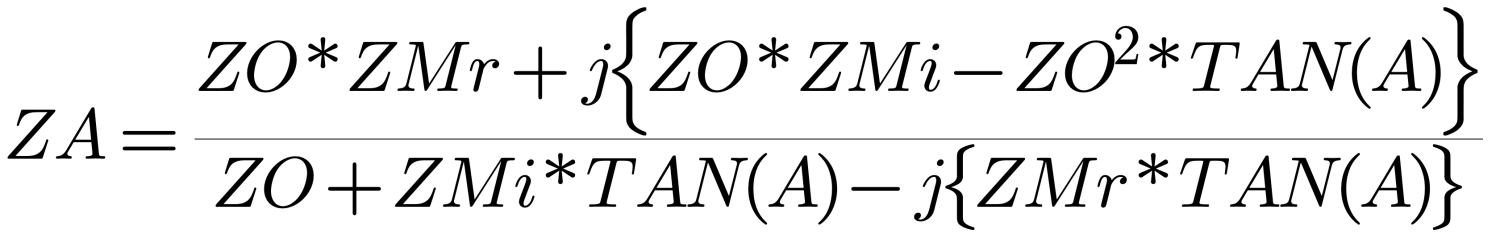
Applying the Complex Conjugate operation, Equation 4 (Figure 4a) then becomes:

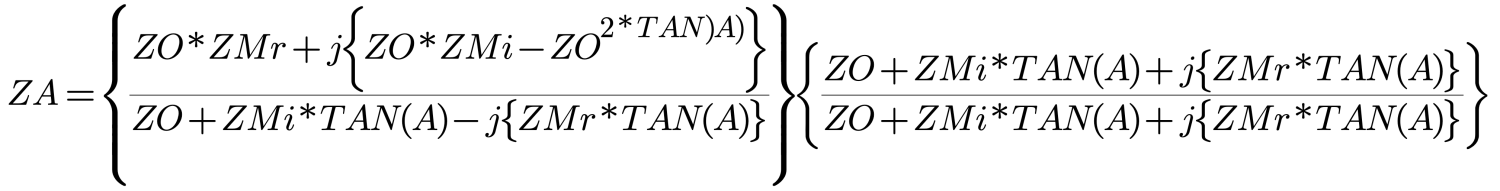
Which is then ‘reduced’ to:

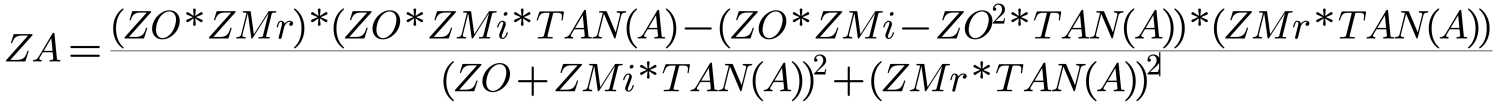
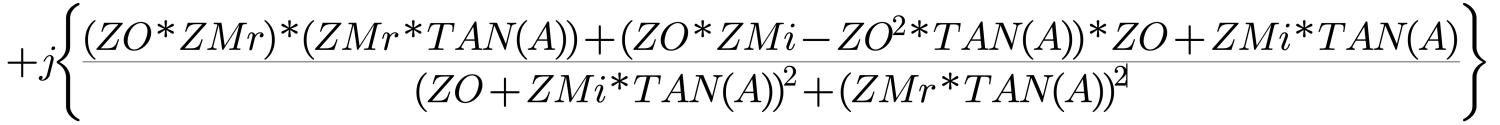
Although this looks somewhat tenuous, close inspection will show that the first part contains only real terms (i.e., no j’s), and the second part is imaginary. It must be remembered that ZMi is only a magnitude … the imaginary piece of it, the j, has been removed by manipulation via the Complex Conjugate.

There is a recurrence of common terms throughout Equation 5 (Figure 5a and 5b) so substitutions are made to make things neater:

They are:

R1 = ZMr*ZO
R2 = ZO + ZMi*TAN(A)
R3 = ZMi*ZO – ZO²*TAN(A)
R4 = ZMr_TAN(A)

Equation 5 now becomes:

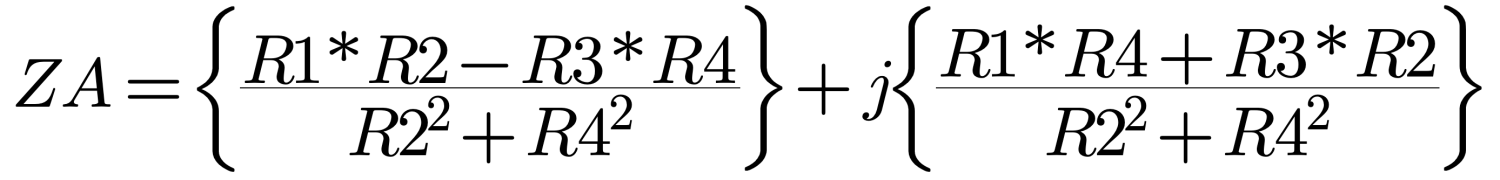
Which is easily manipulated by a home computer by treating the real and imaginary terms separately. The only thing complex about Equation 6 (Figure 6) is the j operator. The term following the j is only a magnitude, just as is the real part of the Equation. The computer only uses the j when it prints out the results by inserting it in front of the second term.

Program version I

Listing 1 is a simple BASIC routine which was coded to solve Equation 3 (Figure 3) for the feed point impedance. It works by using Equation 6 (Figure 6) with identified substitutions. Also included is the option to calculate a coaxial series section transformer matching section to match the line to just determined feed point impedance. This optional part of the program was coded from reference 1. There are some requirements which must be levied on the impedance of the matching section, and these are described in the reference article.

The program was written on a Tandy 1000 in GW-BASIC but should be transportable to most other BASIC versions. A few comments about the program are in order:

Useable results are obtained even though precision and variables are not defined; elegance is not required here.
The Program calculates the electrical length of the feed line in degrees based on its physical length, velocity factor, and frequency of measurement. A noise-bridge can be used to determine the electrical length directly if a record of the length and velocity factor of the feed line used in each antenna installation is not available. See the handbook or any noise-bridge manual for instructions. This program should be easily convertible to ask for the electrical length.
The Program is menu driven and should therefore be easy to use.

Figure 1 shows a sample run.

Program version II

Although Version 1 does a good job, it was still cumbersome to use over and over with only small changes in input data. Rather than rewrite it to smooth its use, another approach was incorporated via a spreadsheet. These can be designed to display the desired data simultaneously and continuously and are extremely fast. Listing 2 is a cell-by-cell itemization of the spreadsheet, coded from the BASIC listing and works with LOTUS and TWIN, and probably most of the others. Public Domain Software sells a LOTUS clone called AS-EASY-AS for $5.00 Figure 2 shows a sample run.

At this point I should say that I am missing LISTING 1, LISTING 2, Figure 1 and Figure 2, these were not backed up and I do not have these so if anyone does, I would really like to complete this posting.

The four missing links were as follows:

Listing 1 : http://www.antennex.com/archival/archive2/Folder01/hoffman/listing1.htm

Listing 2 : http://www.antennex.com/archival/archive2/Folder01/hoffman/listing2.htm

Figure 1 : http://www.antennex.com/archival/archive2/Folder01/hoffman/figure01.htm

Figure 2 : http://www.antennex.com/archival/archive2/Folder01/hoffman/figure01.htm

All the Input/Output data is placed in a section of the spreadsheet which is seen on the screen. The calculations are placed in cells which are external to those which are normally displayed, keeping the display neat and uncluttered.

Some Comments about Listing 2:

The first two alpha numeric digits followed by a colon designate the cells location.
The apostrophe (‘) designates that the cell entry is textual. It’s an artefact of the spreadsheet listing procedure and should not be entered into a cell.
Cells with numerical entries only are the input data cells. The numbers in these cells are not magical… they will change as soon as you insert your data for your particular problems.
Ignore the ‘ERR’ messages that show up in various cells as you enter them. These are due to the cells trying to perform operations using data from cells that haven’t been created. These messages will clear themselves as the cells all get entered.
Figure 3 is cross referenced which correlates the various cell entries to their respective BASIC lines from Listing 1. This will be useful for those who wish to modify either of the programs.
Actual antenna feed point impedance values may be entered directly into cells E16 and G16 in cases where a remote measurement is not needed to determine the impedance.
Cells E15 and G15 are what I call reminder cells. They reference the cells which are called by cellsE16 and G16 during the default mode of automatic feed point impedance calculation. If you invoke the option described in Note 7. Above, and then want to go back to auto calculation of the feed point impedance, type “+L21” (referenced by cell E15) into cell E16 and “+L22” (referenced by cell G15) into cell G16.

References

ARRL Handbook, Edition 14, Page 5-10.
Ham Radio Magazine, November 1984, p. 106
Public Domain Software, P.O. Box 51315, Indianapolis, IN 46251

Another missing link I am afraid:

Figure 3 : http://www.antennex.com/archival/archive2/Folder01/hoffman/figure03.htm

Originally posted on the AntennaX Online Magazine by Roger J. Hoffman, WB9BXT – This was a bit of a nightmare as the pages on the web were actual poor quality images so I am afraid that I had tio copy all of the information out so if there are any problems here, please let me know, I am hoping that someone will either send me a copy of the AntenneX CD-ROM or at the least let me have a copy of the missing information, I still feel that there is enough good information in this article that made it worth posting. James, MD0MDI

Last Updated : 18th April 2024